Functional Programming

What is functional programming?

We've got quite far into the tutorial, yet we haven't really considered functional programming. All of the features given so far - rich data types, pattern matching, type inference, nested functions - you could imagine could exist in a kind of "super C" language. These are Cool Features certainly, and make your code concise, easy to read, and have fewer bugs, but they actually have very little to do with functional programming. In fact my argument is going to be that the reason that functional languages are so great is not because of functional programming, but because we've been stuck with C-like languages for years and in the meantime the cutting edge of programming has moved on considerably. So while we were writing struct { int type; union { ... } } for the umpteenth time, ML and Haskell programmers had safe variants and pattern matching on datatypes. While we were being careful to free all our mallocs, there have been languages with garbage collectors able to outperform hand-coding since the 80s.

Well, after that I'd better tell you what functional programming is anyhow.

The basic, and not very enlightening definition is this: in a functional language, functions are first-class citizens.

Lot of words there that don't really make much sense. So let's have an example:

# let double x = x * 2 in
  List.map double [ 1; 2; 3 ];;
- : int list = [2; 4; 6]

In this example, I've first defined a nested function called double which takes an argument x and returns x * 2. Then map calls double on each element of the given list ([1; 2; 3]) to produce the result: a list with each number doubled.

map is known as a higher-order function (HOF). Higher-order functions are just a fancy way of saying that the function takes a function as one of its arguments.

So far so simple. If you're familiar with C/C++ then this looks like passing a function pointer around. Java has some sort of abomination called an anonymous class which is like a dumbed-down, slow and long-winded closure. If you know Perl then you probably already know and use Perl's closures and Perl's map function, which is exactly what we're talking about. The fact is that Perl is actually quite a good functional language.

Closures are functions which carry around some of the "environment" in which they were defined. In particular, a closure can reference variables which were available at the point of its definition. Let's generalise the function above so that now we can take any list of integers and multiply each element by an arbitrary value n:

# let multiply n list =
    let f x =
      n * x in
    List.map f list;;
val multiply : int -> int list -> int list = <fun>

Hence:

# multiply 2 [1; 2; 3];;
- : int list = [2; 4; 6]
# multiply 5 [1; 2; 3];;
- : int list = [5; 10; 15]

The important point to note about the multiply function is the nested function f. This is a closure. Look at how f uses the value of n which isn't actually passed as an explicit argument to f. Instead f picks it up from its environment - it's an argument to the multiply function and hence available within this function.

This might sound straightforward, but let's look a bit closer at that call to map: List.map f list.

map is defined in the List module, far away from the current code. In other words, we're passing f into a module defined "a long time ago, in a galaxy far far away". For all we know that code might pass f to other modules, or save a reference to f somewhere and call it later. Whether it does this or not, the closure will ensure that f always has access back to its parental environment, and to n.

Here's a real example from lablgtk. This is actually a method on a class (we haven't talked about classes and objects yet, but just think of it as a function definition for now).

class html_skel obj = object (self)
  ...
  ...
  method save_to_channel chan =
    let receiver_fn content =
      output_string chan content;
      true in
    save obj receiver_fn
  ...
end

First of all you need to know that the save function called at the end of the method takes as its second argument a function (receiver_fn). It repeatedly calls receiver_fn with snippets of text from the widget that it's trying to save.

Now look at the definition of receiver_fn. This function is a closure alright because it keeps a reference to chan from its environment.

Partial function applications and currying

Let's define a plus function which just adds two integers:

# let plus a b =
    a + b;;
val plus : int -> int -> int = <fun>

Some questions for people asleep at the back of the class.

What is plus?
What is plus 2 3?
What is plus 2?

Question 1 is easy. plus is a function, it takes two arguments which are integers and it returns an integer. We write its type like this:

plus : int -> int -> int

Question 2 is even easier. plus 2 3 is a number, the integer 5. We write its value and type like this:

5 : int

But what about question 3? It looks like plus 2 is a mistake, a bug. In fact, however, it isn't. If we type this into the OCaml interactive toplevel, it tells us:

# plus 2;;
- : int -> int = <fun>

This isn't an error. It's telling us that plus 2 is in fact a function, which takes an int and returns an int. What sort of function is this? We experiment by first of all giving this mysterious function a name (f), and then trying it out on a few integers to see what it does:

# let f = plus 2;;
val f : int -> int = <fun>
# f 10;;
- : int = 12
# f 15;;
- : int = 17
# f 99;;
- : int = 101

In engineering this is sufficient proof by example for us to state that plus 2 is the function which adds 2 to things.

Going back to the original definition, let's "fill in" the first argument (a) setting it to 2 to get:

let plus 2 b =       (* This is not real OCaml code! *)
  2 + b

You can kind of see, I hope, why plus 2 is the function which adds 2 to things.

Looking at the types of these expressions we may be able to see some rationale for the strange -> arrow notation used for function types:

    plus : int -> int -> int
  plus 2 : int -> int
plus 2 3 : int

This process is called currying (or perhaps it's called uncurrying, I never was really sure which was which). It is called this after Haskell Curry who did some important stuff related to the lambda calculus. Since I'm trying to avoid entering into the mathematics behind OCaml because that makes for a very boring and irrelevant tutorial, I won't go any further on the subject. You can find much more information about currying if it interests you by doing a search on Google.

Remember our double and multiply functions from earlier on? multiply was defined as this:

# let multiply n list =
    let f x =
      n * x in
    List.map f list;;
val multiply : int -> int list -> int list = <fun>

We can now define double, triple &c functions very easily just like this:

# let double = multiply 2;;
val double : int list -> int list = <fun>
# let triple = multiply 3;;
val triple : int list -> int list = <fun>

They really are functions, look:

# double [1; 2; 3];;
- : int list = [2; 4; 6]
# triple [1; 2; 3];;
- : int list = [3; 6; 9]

You can also use partial application directly (without the intermediate f function) like this:

# let multiply n = List.map (( * ) n);;
val multiply : int -> int list -> int list = <fun>
# let double = multiply 2;;
val double : int list -> int list = <fun>
# let triple = multiply 3;;
val triple : int list -> int list = <fun>
# double [1; 2; 3];;
- : int list = [2; 4; 6]
# triple [1; 2; 3];;
- : int list = [3; 6; 9]

In the example above, (( * ) n) is the partial application of the ( * ) (times) function. Note the extra spaces needed so that OCaml doesn't think (* starts a comment.

You can put infix operators into brackets to make functions. Here's an identical definition of the plus function as before:

# let plus = ( + );;
val plus : int -> int -> int = <fun>
# plus 2 3;;
- : int = 5

Here's some more currying fun:

# List.map (plus 2) [1; 2; 3];;
- : int list = [3; 4; 5]
# let list_of_functions = List.map plus [1; 2; 3];;
val list_of_functions : (int -> int) list = [<fun>; <fun>; <fun>]

What is functional programming good for?

Functional programming, like any good programming technique, is a useful tool in your armoury for solving some classes of problems. It's very good for callbacks, which have multiple uses from GUIs through to event-driven loops. It's great for expressing generic algorithms. List.map is really a generic algorithm for applying functions over any type of list. Similarly you can define generic functions over trees. Certain types of numerical problems can be solved more quickly with functional programming (for example, numerically calculating the derivative of a mathematical function).

Pure and impure functional programming

A pure function is one without any side-effects. A side-effect really means that the function keeps some sort of hidden state inside it. strlen is a good example of a pure function in C. If you call strlen with the same string, it always returns the same length. The output of strlen (the length) only depends on the inputs (the string) and nothing else. Many functions in C are, unfortunately, impure. For example, malloc - if you call it with the same number, it certainly won't return the same pointer to you. malloc, of course, relies on a huge amount of hidden internal state (objects allocated on the heap, the allocation method in use, grabbing pages from the operating system, etc.).

ML-derived languages like OCaml are "mostly pure". They allow side-effects through things like references and arrays, but by and large most of the code you'll write will be pure functional because they encourage this thinking. Haskell, another functional language, is pure functional. OCaml is therefore more practical because writing impure functions is sometimes useful.

There are various theoretical advantages of having pure functions. One advantage is that if a function is pure, then if it is called several times with the same arguments, the compiler only needs to actually call the function once. A good example in C is:

for (i = 0; i < strlen (s); ++i)
  {
    // Do something which doesn't affect s.
  }

If naively compiled, this loop is O(n²) because strlen (s) is called each time and strlen needs to iterate over the whole of s. If the compiler is smart enough to work out that strlen is pure functional and that s is not updated in the loop, then it can remove the redundant extra calls to strlen and make the loop O(n). Do compilers really do this? In the case of strlen yes, in other cases, probably not.

Concentrating on writing small pure functions allows you to construct reusable code using a bottom-up approach, testing each small function as you go along. The current fashion is for carefully planning your programs using a top-down approach, but in the author's opinion this often results in projects failing.

Strictness vs laziness

C-derived and ML-derived languages are strict. Haskell and Miranda are non-strict, or lazy, languages. OCaml is strict by default but allows a lazy style of programming where it is needed.

In a strict language, arguments to functions are always evaluated first, and the results are then passed to the function. For example in a strict language, the call give_me_a_three (1/0) is always going to result in a divide-by-zero error:

# let give_me_a_three _ = 3;;
val give_me_a_three : 'a -> int = <fun>
# give_me_a_three (1/0);;
Exception: Division_by_zero.

If you've programmed in any conventional language, this is just how things work, and you'd be surprised that things could work any other way.

In a lazy language, something stranger happens. Arguments to functions are only evaluated if the function actually uses them. Remember that the give_me_a_three function throws away its argument and always returns a 3? Well in a lazy language, the above call would not fail because give_me_a_three never looks at its first argument, so the first argument is never evaluated, so the division by zero doesn't happen.

Lazy languages also let you do really odd things like defining an infinitely long list. Provided you don't actually try to iterate over the whole list this works (say, instead, that you just try to fetch the first 10 elements).

OCaml is a strict language, but has a Lazy module that lets you write lazy expressions. Here's an example. First we create a lazy expression for 1/0:

# let lazy_expr = lazy (1/0);;
val lazy_expr : int lazy_t = <lazy>

Notice the type of this lazy expression is int lazy_t.

Because give_me_a_three takes 'a (any type) we can pass this lazy expression into the function:

# give_me_a_three lazy_expr;;
- : int = 3

To evaluate a lazy expression, you must use the Lazy.force function:

# Lazy.force lazy_expr;;
Exception: Division_by_zero.

Boxed vs. unboxed types

One term which you'll hear a lot when discussing functional languages is "boxed". I was very confused when I first heard this term, but in fact the distinction between boxed and unboxed types is quite simple if you've used C, C++ or Java before (in Perl, everything is boxed).

The way to think of a boxed object is to think of an object which has been allocated on the heap using malloc in C (or equivalently new in C++), and/or is referred to through a pointer. Take a look at this example C program:

#include <stdio.h>

void
printit (int *ptr)
{
  printf ("the number is %d\n", *ptr);
}

void
main ()
{
  int a = 3;
  int *p = &a;

  printit (p);
}

The variable a is allocated on the stack, and is quite definitely unboxed.

The function printit takes a boxed integer and prints it.

The diagram below shows an array of unboxed (top) vs. boxed (below) integers:

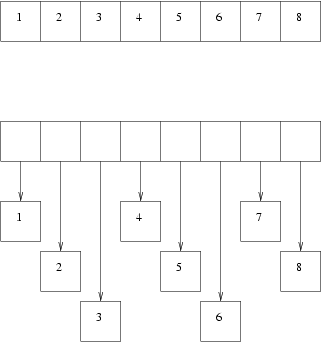
Boxed Array

No prizes for guessing that the array of unboxed integers is much faster than the array of boxed integers. In addition, because there are fewer separate allocations, garbage collection is much faster and simpler on the array of unboxed objects.

In C or C++ you should have no problems constructing either of the two types of arrays above. In Java, you have two types, int which is unboxed and Integer which is boxed, and hence considerably less efficient. In OCaml, the basic types are all unboxed.